形式系统

给出右线性文法：
S à 0S | 1S | 1A | 0B

A à 1C | 1

B à 0C | 0

C à 0C | 1C | 0 | 1

右线性文法特点：终结符＋非终结符，

1、由右线性文法构造NFA：

1）  每个非终结符在图中对应一个结点，文法开始符号表示图中的初态结点，添加一终态结点 Z 。

2）  对形如 A à cB 的产生式，画一 A 到 C 的弧，标记为 c 。

3）  对形如 A à c 的产生式，画一 A 到 Z 的弧，标记为 c 。

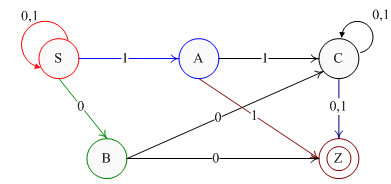
(作为例子，请注意文法和图中彩色部分对应)

2 、由 NFA 转化为 DFA

       其实质是将结点的跳转转化为结点集之间的跳转。由初始结点 S 出发，找出其闭包构成的集合，在本例中， 由于不含ε路径，S的闭包集合就是 {S}。然后由{S}出发，找出通过不同的路径所能到达的集合。
      为清晰起见，将选择图中一个集合跳转，重新标上颜色，和下表对应。
   

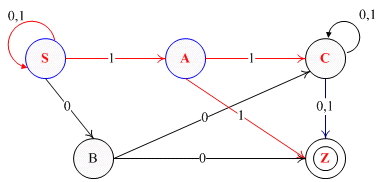
集合编号	集合	0	1
S0	{S}	{S,B}	{S,A}
S1	{S,B}	{S,B,C,Z}	{S,A}
S2	{S,A}	{S,B}	{S,A,C,Z}
S3	{S,B,C,Z}	{S,B,C,Z}	{S,A,C,Z}
S4	{S,A,C,Z}	{S,B,C,Z}	{S,A,C,Z}

3 、最小化

最小化的思想是在不改变 DFA 识别的语言的前提下，合并相应的结点，使合并后的 DFA 与合并前的 DFA 等效，而结点数目减少。

但在实现上，采用是从合到分的方法。先从最精简的结构出发，即，整个系统就两个集合，所有的终态结点并为一个结点，所有的非综态结点合并为一个结点 ( 整个系统不可能合并为一个结点，因为如果是一个结点的话，任何弧只能指向这个唯一的结点，本算法失效，但会不会出现只有一个结点的情况？大家想想。比如该 DFA 所定义的语言为 { ε } ，如果是这样，能否和本算法统一？ ) 。

然后看这种划分是否可行，如不可行，再分解出更多的集合。而合并可行的依据就是集合中的每个元素通过同一条弧到达同一个目标集合。

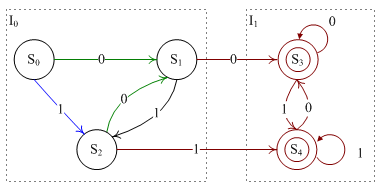
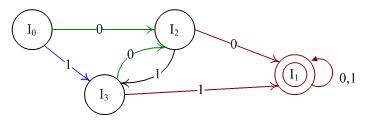
如上图，首先将所有的非综态结点合并为 I₀ ，。将综态结点合并为 I₁ 。分别考察两个集合。对于 I₀ ，通过 0 弧，有如下跳转： S₀ à S₁ ， S₂ à S₁ ， S₁ à S₃ 。而 S₁ ∈ I₀ ， S₃ ∈ I₁ ，据此， S₁ 和 S₀ 、 S₂ 要分开位于不同集合。

现假定 I₀={ S₀ ,S₂} ， I₁={ S₃ ,S₄} ， I₂ ＝ { S₁ } 。考察 I₀ ，同样是通过 1 弧，则有如下跳转：

S₀ à S₂ 、 S₂ à S₄ ，而 S₂ ∈I ₀ ,S₄∈I ₁ 。故， S₂ 与 S₄ 分开。可以看出，只要发现一条弧不满足上述条件，就可以将其分离。并非要考察完每条弧。

       再来考察 I₁ ，通过 0 弧可得： S₃ à S₃ ∈ I₁ ， S₄ à S₃ ∈ I₁ 。通过 1 弧可得： S₃ à S₄ ∈ I₁ ， S₃ à S₄ ∈ I₁ 。显然， I₁ 不可再分。

       如此重复，直到每个集合 I_i ( I=0,1,…) 均不可再分为止。

最小化后的状态转换图如下：